A Fórmula da Área do Triângulo que Você Precisa Saber
Bora descomplicar a matemática, migas! A área do triângulo pode parecer um bicho de sete cabeças, mas juro que é mais fácil do que parece! Se você sempre se enrola nas fórmulas e não sabe por onde começar quando precisa calcular a área de um triângulo, chegou ao lugar certo. Esquece aquela dor de cabeça com números e símbolos! Aqui, vamos desvendar tudo de um jeito simples, direto e sem enrolação, para você nunca mais travar na hora de resolver um probleminha de geometria.
A Fórmula da Área do Triângulo que Você Precisa Saber
Desvendando a Área do Triângulo: O Bê-á-bá que Ninguém Te Contou!
Acredite em mim, calcular a área do triângulo não precisa ser um pesadelo. É muito mais simples do que você imagina! A fórmula básica é como uma receita de bolo: simples de aprender e fácil de aplicar. Com ela, você consegue descobrir o espaço ocupado por qualquer triângulo, seja ele grande, pequeno, gordinho ou magrinho. O segredo está em entender os componentes da fórmula e como identificá-los em cada triângulo. Vamos começar pelo básico, que é o que realmente importa!
O Que é a Área do Triângulo, Afinal?
A área, em termos simples, é a medida da superfície interna de uma figura geométrica. Imagine que você está pintando um triângulo em uma parede. A área é a quantidade de tinta que você vai usar para cobrir toda a superfície desse triângulo. No caso do triângulo, a área é a quantidade de espaço que ele ocupa em um plano. É uma medida bidimensional, ou seja, ela leva em consideração o comprimento e a largura. Entender o conceito de área é crucial não só para matemática, mas também para diversas outras áreas, como arquitetura, design e até mesmo no seu dia a dia, ao calcular a quantidade de material necessário para um projeto.
A Fórmula Mágica da Área do Triângulo
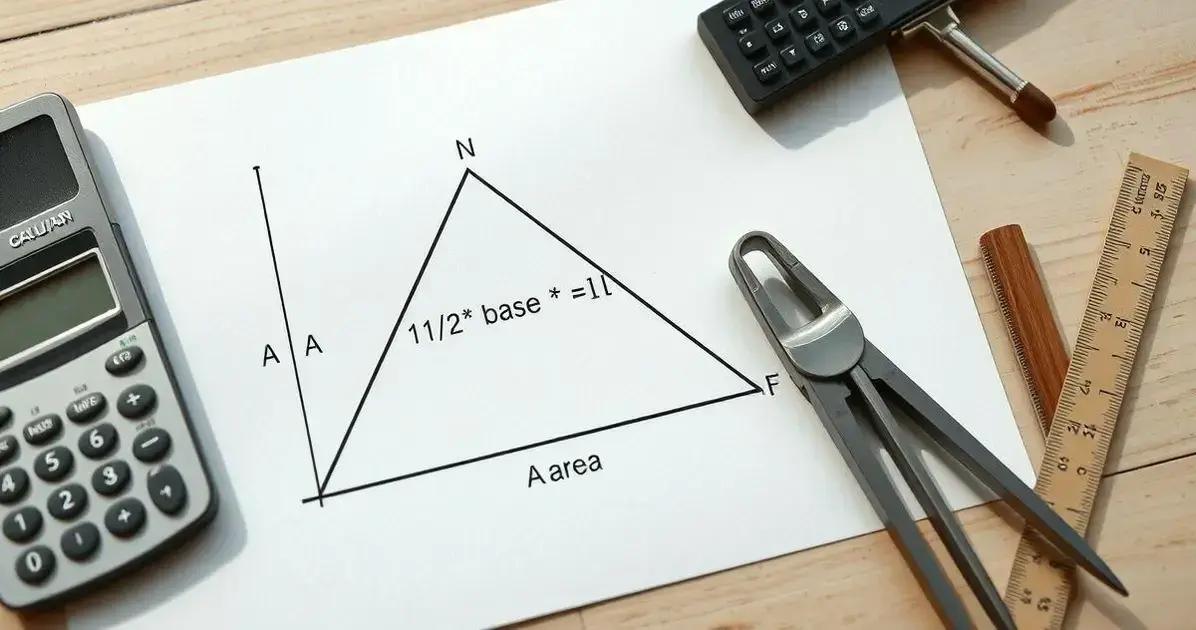
A fórmula básica da área do triângulo é:
Área = (Base x Altura) / 2
- Base: É o lado do triângulo que você escolhe como referência. É como a linha de baixo do triângulo, onde ele está “apoiado”.
- Altura: É a distância perpendicular (formando um ângulo de 90 graus) entre a base e o vértice oposto (a ponta) do triângulo. Imagine uma linha reta que sai da ponta do triângulo e vai até a base, formando um ângulo reto. Essa linha é a altura.
- / 2: A divisão por dois é porque um triângulo pode ser visto como a metade de um retângulo ou paralelogramo.
Simples assim! Parece complicado, mas com alguns exemplos e um pouco de prática, você vai dominar a fórmula e calcular a área de qualquer triângulo rapidinho.
Como Identificar a Base e a Altura do Triângulo
Identificar a base e a altura pode ser o “pulo do gato” na hora de calcular a área. A base é, geralmente, o lado que está na parte inferior do triângulo, mas você pode escolher qualquer lado como base. A altura, como já falamos, é a linha que sai do vértice oposto à base e forma um ângulo de 90 graus com ela. Em alguns triângulos, a altura já vem desenhada, em outros, você precisa traçá-la. Se o triângulo for reto (com um ângulo de 90 graus), a altura será um dos lados que formam esse ângulo. Em triângulos obtusos (com um ângulo maior que 90 graus), a altura pode ficar fora do triângulo, sendo traçada a partir do vértice até o prolongamento da base.
Para facilitar, imagine que a base é o chão e a altura é o quão alto o triângulo é. Com a prática, você vai conseguir identificar a base e a altura de qualquer triângulo, sem precisar pensar muito. Não se preocupe se no começo parecer confuso, o importante é praticar e entender o conceito. Com o tempo, a identificação da base e da altura se tornará algo natural.
Exemplos Práticos: Calculando a Área do Triângulo na Prática
Vamos colocar a mão na massa com alguns exemplos!
Exemplo 1:
- Base = 10 cm
- Altura = 5 cm
Área = (10 cm x 5 cm) / 2 = 25 cm²
Exemplo 2:
- Base = 8 cm
- Altura = 6 cm
Área = (8 cm x 6 cm) / 2 = 24 cm²
Viu como é fácil? Basta multiplicar a base pela altura e dividir por dois. A unidade de medida da área sempre será ao quadrado (cm², m², etc.), porque estamos medindo uma superfície bidimensional. Com esses exemplos, você já tem uma base sólida para calcular a área de qualquer triângulo.
Se você gostou de aprender sobre a fórmula básica da área do triângulo, que tal a gente ir além e explorar as variações da fórmula para diferentes tipos de triângulos?
Tipos de Triângulos e Suas Fórmulas Específicas: Aprofundando o Conhecimento!
Nem todos os triângulos são iguais, né? Existem vários tipos, e cada um tem suas particularidades. Para calcular a área de cada tipo, às vezes, precisamos de uma “ajudinha” extra na fórmula. Vamos explorar os principais tipos de triângulos e suas fórmulas, para que você esteja preparada para qualquer desafio!
Triângulo Retângulo: O Que Muda na Hora de Calcular?
O triângulo retângulo é aquele que possui um ângulo reto, ou seja, um ângulo de 90 graus. Ele é bem fácil de identificar, porque parece um “L” ou um “canto de parede”. A boa notícia é que, para calcular a área do triângulo retângulo, a fórmula básica continua valendo, mas com uma simplificação. Os lados que formam o ângulo reto (os catetos) são a base e a altura do triângulo. Então, basta multiplicar um cateto pelo outro e dividir por dois.
Por exemplo, se um cateto mede 3 cm e o outro mede 4 cm, a área será (3 cm x 4 cm) / 2 = 6 cm². Simples assim! A vantagem do triângulo retângulo é que a altura já está bem definida, facilitando o cálculo.
Triângulo Equilátero: A Fórmula Especial para Lados Iguais
O triângulo equilátero é aquele que possui todos os três lados com a mesma medida. Ele é bem simétrico e charmoso! Para calcular a área do triângulo equilátero, podemos usar a fórmula tradicional (base x altura / 2), mas também existe uma fórmula específica que usa apenas a medida do lado:
Área = (lado² x √3) / 4
Onde:
- lado é a medida de um dos lados do triângulo (já que todos são iguais)
- √3 é a raiz quadrada de 3 (aproximadamente 1,732)
Essa fórmula é muito útil quando você só tem a medida do lado do triângulo. Por exemplo, se o lado do triângulo equilátero mede 5 cm, a área será (5² x √3) / 4 = (25 x 1,732) / 4 = 10,825 cm².
Triângulo Isósceles: Como Calcular a Área?
O triângulo isósceles tem dois lados com a mesma medida e um lado diferente. Para calcular a área, você pode usar a fórmula básica (base x altura / 2), mas a dificuldade pode estar em encontrar a altura. Em um triângulo isósceles, a altura divide a base ao meio, formando dois triângulos retângulos. Você pode usar o Teorema de Pitágoras para calcular a altura, se precisar, ou buscar a informação no enunciado do problema.
Vamos supor que a base do triângulo isósceles mede 6 cm e a altura mede 4 cm. A área será (6 cm x 4 cm) / 2 = 12 cm².
Triângulo Escaleno: Lidando com Lados Diferentes
O triângulo escaleno é aquele que possui todos os lados com medidas diferentes. Calcular a área do triângulo escaleno pode parecer um pouco mais desafiador, mas a fórmula básica (base x altura / 2) continua sendo a chave. A dificuldade, geralmente, está em identificar a altura, que nem sempre é dada no problema. Em alguns casos, pode ser necessário usar o Teorema de Pitágoras ou outras técnicas para encontrar a altura.
Se você tiver a base e a altura, o cálculo da área é direto. Se não tiver a altura, precisará encontrar outra forma de calcular, dependendo das informações que você tem (medida dos lados e dos ângulos, por exemplo).
A Importância da Unidade de Medida na Área do Triângulo
Nunca se esqueça da unidade de medida! A área é sempre expressa em unidades quadradas (cm², m², km², etc.). Isso porque estamos medindo uma superfície, que tem duas dimensões: comprimento e largura. Se você estiver trabalhando com centímetros, a área será em centímetros quadrados. Se estiver trabalhando com metros, a área será em metros quadrados. A unidade de medida é crucial para que você possa entender o tamanho da área que você calculou e também para comparar com outras áreas.
Se você está gostando de aprender sobre os diferentes tipos de triângulos, que tal a gente dar uma olhadinha em alguns exemplos práticos de como calcular a área do triângulo no dia a dia?
A Área do Triângulo no Dia a Dia: Onde Você Encontra Essa Matemática?
A área do triângulo está mais presente na nossa vida do que imaginamos! Ela está em diversos lugares, desde a arquitetura da sua casa até na fatia de pizza que você come. Vamos explorar algumas situações cotidianas em que a área do triângulo faz toda a diferença:
Arquitetura e Construção: Planejando Espaços
Na arquitetura e na construção, a área do triângulo é usada para calcular a quantidade de material necessário para construir telhados em forma de triângulo, fachadas com design triangular e até mesmo para otimizar o uso de espaço em projetos. Os arquitetos e engenheiros usam a área do triângulo para planejar e dimensionar estruturas, garantindo que elas sejam estáveis e eficientes.
Design de Interiores: Criando Ambientes Harmônicos
No design de interiores, a área do triângulo pode ser usada para calcular a área de paredes triangulares, como as de um sótão, ou para determinar o tamanho ideal de objetos decorativos com formatos triangulares, como espelhos, quadros ou prateleiras. O design de interiores usa a área do triângulo para criar ambientes equilibrados e visualmente agradáveis.
Artesanato e Costura: Modelando com Precisão
Se você gosta de artesanato e costura, a área do triângulo pode ser útil para calcular a quantidade de tecido necessária para fazer um painel, um vestido ou um enfeite com formato triangular. A área do triângulo ajuda a planejar e cortar o tecido com precisão, evitando desperdícios e garantindo que o resultado final fique perfeito.
Culinária: Fatias de Pizza e Outras Delícias
Até na culinária a área do triângulo aparece! Ao cortar uma pizza em fatias, cada fatia tem um formato triangular. Calcular a área de cada fatia pode ser interessante para entender a proporção da pizza e para comparar o tamanho das fatias. A área do triângulo também pode ser usada para calcular o volume de um cone de sorvete.
Jardins e Paisagismo: Planejando o Espaço Verde
No paisagismo, a área do triângulo pode ser usada para calcular a área de canteiros triangulares, para determinar a quantidade de terra, adubo e plantas necessárias para preencher um espaço, ou para planejar o design de um jardim com formatos geométricos.
Jogos e Quebra-cabeças: Desafiando a Mente
A área do triângulo também aparece em jogos e quebra-cabeças que envolvem formas geométricas. Calcular a área de um triângulo pode ser a chave para resolver um desafio e para desenvolver o raciocínio lógico.
E muito mais…
A área do triângulo está presente em diversas outras áreas do nosso dia a dia, como na engenharia, na geografia, na física e na programação. Saber calcular a área do triângulo é uma habilidade útil e versátil, que pode ser aplicada em diferentes situações.
Se você está se sentindo confiante com a área do triângulo, que tal praticar com alguns exemplos e exercícios?
Dicas Extras e Exercícios Práticos para Você Arrasar na Área do Triângulo!
Agora que você já sabe a fórmula, os tipos de triângulos e onde a área do triângulo aparece no dia a dia, vamos turbinar o seu conhecimento com algumas dicas extras e exercícios práticos para você arrasar de vez!
Dicas para Facilitar os Cálculos da Área do Triângulo
- Desenhe o triângulo: Sempre que possível, desenhe o triângulo. Isso te ajudará a visualizar a base e a altura, e a entender melhor a forma geométrica.
- Identifique a base e a altura com cuidado: Preste atenção em como a altura se relaciona com a base. A altura deve formar um ângulo reto (90 graus) com a base.
- Use a calculadora: Não tenha medo de usar a calculadora! Ela é uma ferramenta poderosa para fazer os cálculos de forma rápida e precisa.
- Revise as unidades de medida: Certifique-se de que todas as medidas estão na mesma unidade (cm, m, km, etc.) antes de fazer os cálculos.
- Pratique, pratique, pratique: A prática leva à perfeição! Quanto mais você praticar, mais fácil será calcular a área do triângulo.
- Procure por exemplos: Explore exemplos de como a área do triângulo é usada em diferentes contextos.
- Aproveite as ferramentas online: Use ferramentas online para verificar seus cálculos e para aprender mais sobre a área do triângulo.
Exercícios Práticos para Treinar: Coloque a Mão na Massa!
Vamos colocar em prática o que aprendemos! Resolva os exercícios abaixo e veja como você está indo.
Exercício 1:
Calcule a área de um triângulo com base de 12 cm e altura de 8 cm.
Exercício 2:
Um triângulo retângulo tem catetos que medem 5 cm e 10 cm. Qual é a área do triângulo?
Exercício 3:
Um triângulo equilátero tem lados que medem 6 cm. Qual é a área do triângulo? (Use a fórmula específica para triângulos equiláteros)
Exercício 4:
Um triângulo isósceles tem base de 10 cm e altura de 7 cm. Qual é a área do triângulo?
Exercício 5:
Calcule a área de um triângulo com base de 15 cm e altura de 9 cm.
Respostas:
- 48 cm²
- 25 cm²
- 15,59 cm² (aproximadamente)
- 35 cm²
- 67,5 cm²
Dicas para Estudar e Memorizar a Fórmula da Área do Triângulo
- Crie um mapa mental: Faça um mapa mental com a fórmula da área do triângulo, os tipos de triângulos e as aplicações no dia a dia.
- Faça flashcards: Crie flashcards com a fórmula, os exemplos e os exercícios.
- Explique para alguém: Tente explicar a fórmula e os conceitos para outra pessoa. Isso te ajudará a fixar o conhecimento.
- Assista a vídeos: Assista a vídeos explicativos sobre a área do triângulo.
- Faça resumos: Faça resumos dos conceitos importantes.
- Use a criatividade: Crie seus próprios exemplos e exercícios.
Com essas dicas e exercícios, você estará pronta para dominar a área do triângulo de uma vez por todas!
Tabela de Fórmulas e Dicas Rápidas
Para facilitar ainda mais a sua jornada no mundo da área do triângulo, preparei uma tabela com as principais fórmulas e algumas dicas rápidas para você ter sempre à mão:
| Tipo de Triângulo | Fórmula | Dicas Rápidas |
|---|---|---|
| Geral | Área = (Base x Altura) / 2 | Lembre-se da unidade de medida! Desenhe o triângulo para visualizar a base e a altura. |
| Retângulo | Área = (Cateto 1 x Cateto 2) / 2 | Os catetos são a base e a altura. |
| Equilátero | Área = (Lado² x √3) / 4 | Se souber o lado, use essa fórmula. |
| Isósceles | Área = (Base x Altura) / 2 | A altura divide a base ao meio. Use o Teorema de Pitágoras, se precisar. |
| Escaleno | Área = (Base x Altura) / 2 | A altura nem sempre é dada. Use o Teorema de Pitágoras ou outras técnicas para encontrar a altura. |
Observação: A tabela é apenas um guia rápido. É importante entender os conceitos por trás das fórmulas, e não apenas memorizá-las.
Se você está gostando de aprender sobre a área do triângulo, que tal a gente responder algumas perguntas frequentes sobre o assunto?
Perguntas Frequentes Sobre a Área do Triângulo: Dúvidas Comuns Respondidas!
Para te ajudar a tirar todas as suas dúvidas, separei algumas das perguntas mais comuns sobre a área do triângulo. Vamos lá!
1. Qual a diferença entre área e perímetro?
A área é a medida da superfície interna de uma figura geométrica, enquanto o perímetro é a medida do contorno da figura. Imagine que você está cercando um jardim. A área seria o espaço que o jardim ocupa, e o perímetro seria o comprimento da cerca que você precisa para cercá-lo.
2. Como calcular a área de um triângulo quando a altura não é dada?
Se você não tiver a altura, mas tiver a medida dos lados e dos ângulos, pode usar outras fórmulas, como a fórmula de Heron (que usa a medida dos lados) ou as fórmulas trigonométricas (que usam as medidas dos lados e dos ângulos).
3. O que é o Teorema de Pitágoras e como ele pode ser usado na área do triângulo?
O Teorema de Pitágoras é uma fórmula que relaciona os lados de um triângulo retângulo: a² + b² = c², onde “a” e “b” são os catetos (lados que formam o ângulo reto) e “c” é a hipotenusa (o lado oposto ao ângulo reto). Ele pode ser usado para encontrar a altura de um triângulo, se você souber as medidas dos lados.
4. Qual a importância da unidade de medida na área do triângulo?
A unidade de medida é fundamental para entender o tamanho da área que você calculou e para comparar com outras áreas. A área é sempre expressa em unidades quadradas (cm², m², km², etc.).
5. Como posso praticar e melhorar meus cálculos de área do triângulo?
A prática leva à perfeição! Faça exercícios, desenhe os triângulos, use a calculadora, revise as unidades de medida e explore exemplos do dia a dia.
6. Quais são os principais erros ao calcular a área do triângulo?
Os principais erros são: não identificar corretamente a base e a altura, esquecer de dividir por dois na fórmula, usar unidades de medida incorretas e não prestar atenção aos detalhes do problema.
7. Onde posso encontrar mais informações sobre a área do triângulo?
Você pode encontrar mais informações em livros didáticos, sites de matemática, vídeos educativos e em outros posts do meu blog!
Se você tiver mais alguma dúvida, pode deixar nos comentários!